오늘은 그래프, DFS, BFS에 대해서 공부해보겠습니다!
현재 공부하는데 사용되고 있는 교재는 " 코딩 테스트 합격자 되기 - 자바 편" 입니다. 전에 소개 드렸던 코딩 공부 웹 사이트 중 프로그래머스에서 제공되는 문제들을 풀이해주는 책이라 프로그래머스로 공부하실 때 추천드립니다!!

그래프의 개념
- 노드와 간선을 이용한 비선형 데이터 구조이다.
- 그래프는 데이터 간의 관계를 표현하는데 사용된다.
- 간선은 방향이 있을 수도 없을 수도 있다.
- 관계나 흐름에서 정도를 표현할 필요가 있다면 가중치라는 개념을 추가해서 표현한다.

그래프의 특징과 종류
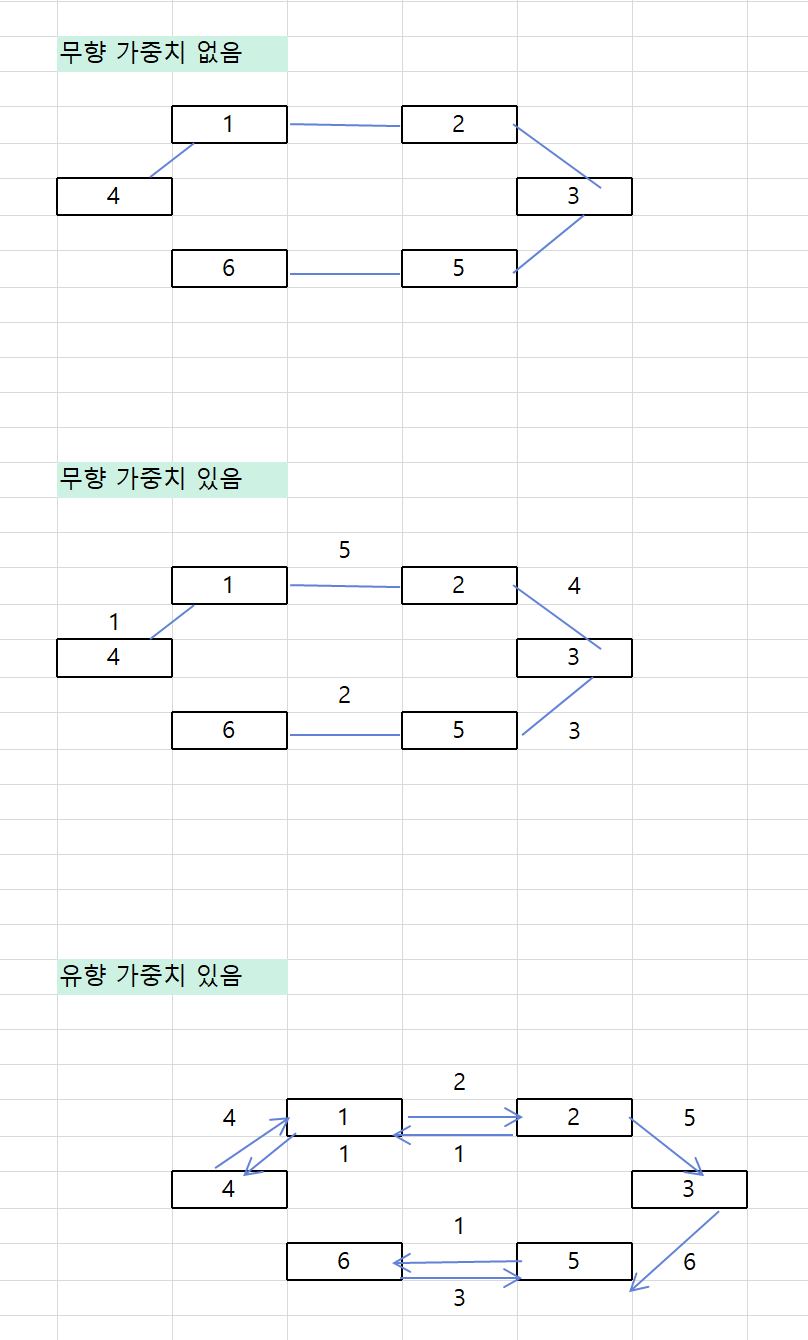
- 그래프는 방향성, 가중치, 순환 특성에 따라 종류를 구분함
- 흐름을 표현하는 방향성
< 방향 그래프 > - 방향이 있는 간선을 포함

- 어느 한쪽으로만 간선이 있는 것이 아니라 서로 반대를 가리키는 간선
< 무방향 그래프 > - 방향이 없는 간선을 포함

2. 흐름의 정도를 표현하는 가중치
< 가중치 그래프 >
- 어떤 데이터는 흐름의 방향뿐 아니라 양도 중요할 수 있다, 그런 정도를 간선에 표현할 때 이를 가중치라고 함

3. 시작과 끝의 연결 여부를 보는 순환
< 순환 그래프 > - 순환이 존재하는 그래프
- 순한 : 특정 노드에서 시작해 간선을 따라 다시 돌아오는 경로가 있는 것

< 비순환 그래프 > 순환이 존재하지않는 그래프



인접 행렬 그래프
인접행렬 : 그래프의 연결 관계를 이차원 배열로 나타내는 방식
adj[i][j] : 노드 i에서 노드j로 가는 간석이 있으면 1, 아니면 0
- 장점
- 2차원 배열에 모든 정점들의 간선 정보가 있기 때문에, 두 정점을 연결하는 간선을 조회할 때 O(1) 시간복잡도로 가능하다.
- 정점(i)의 차수를 구할 때는 다음과 같이 인접행렬(M)의 i번째 행의 값을 모두 더하면 되므로 O(n)의 시간복잡도를 가진다.
- 구현이 비교적 간단하다.
- 단점
- 희소 그래프 표현시 시간 낭비, 노드 값의 차이가 크면 공간 낭비,
- 모든 간선의 수를 알아내려면 인접행렬 전체를 확인해야 하므로 O(n²)의 시간이 소요
인접 리스트 그래프
인접리스트 : 그래프의 연결관계를 vector의 배열로 나타내는 방식 이 때 vector<int>에는 노드의 번호가 직접 저장됨,
그래프는 각 인접리스트에 대한 헤드포인터를 배열로 갖는다
adj[i] : 노드 i에 연결된 노드들을 원소로 갖는 vector
무방향 그래프의 경우 간선이 추가되면 각각의 정점의 인접리스트에 반대편 정점의 노드를 추가해야 한다
- 장점
- 존재하는 간선만 관리하면 되므로 메모리 사용 측명에서 보다 효율적이다.
- 그래프 모든 간선의 수를 알아내려면 각 정점의 헤더 노드부터 모든 인접리스트를 탐색해야하므로 O(n+e)의 시간이 소요
- 단점
- 두 정점을 연결하는 간선을 조회하거나 정점의 차수를 알기 위해서는 정점의 인접 리스트를 탐색해야 하므로 정점의 차수만큼의 시간이 필요하다. O(degree(v))
- 구현이 비교적 어렵다.
인접행렬 VS 인접 리스트

- n : 전체 정점 개수
- e : 전체 간선 개수
- degree(v) : 정점 v에 연결된 간선 수

DFS (깊이 우선 탐색)
- 개념: 한 정점에서 시작해서 한 방향으로 갈 수 있을 만큼 끝까지 탐색한 후, 더 이상 갈 곳이 없으면 이전으로 되돌아와 다른 경로를 탐색하는 방식.
- 특징: 재귀나 스택을 사용해서 구현 가능,
- 깊은 경로 탐색에 적합 (예: 미로 찾기)
- 모든 경로를 다 확인해야 하는 경우 유리
- 최단 거리 보장은 못 함
- 사용 예시: 미로 찾기, 경로 존재 여부 확인 등.
DFS 코드 예시 (재귀 방식) (인접리스트)

✅ 실행 결과: 1 2 4 5 3 (탐색 순서는 그래프 연결 방식에 따라 달라질 수 있음)
BFS (너비 우선 탐색)
- 개념: 시작 정점에서 가까운 노드부터 차례대로 탐색.
- 특징: 큐(Queue)를 이용해서 구현. 먼저 발견한 노드를 먼저 처리 (FIFO 구조)
- 최단 거리 탐색에 적합 (예: 최단 경로 문제)
- 탐색 순서가 계층적 (1단계 → 2단계 → …)
- 메모리 사용량이 DFS보다 많을 수 있음
- 사용 예시: 최단 경로 탐색, 네트워크 연결 확인 등.
BFS 코드 예시(인접 리스트)

✅ 실행 결과: 1 2 3 4 5 (DFS와는 탐색 순서가 다름)
🚩 정리
- DFS: 깊게 파고드는 방식 (재귀/스택 활용)
- BFS: 넓게 퍼지는 방식 (큐 활용)
- 보통 DFS는 경로 탐색, BFS는 최단 거리 탐색에 자주 사용돼요
.🚩 핵심 차이 정리구분 DFS (재귀/스택) BFS (큐)
| 구분 | DFS | BFS |
| 탐색 순서 | 깊이 우선, 한쪽으로 끝까지 감 | 너비 우선, 가까운 노드부터 탐색 |
| 자료구조 | 스택(재귀 호출 스택 포함) | 큐 |
| 용도 | 모든 경로 탐색, 사이클 확인 | 최단 거리 탐색 |
| 결과 | 경로는 찾지만 최단 경로 아님 | 최단 경로 보장 |
👉참고 자료