
📌 들어가며
전에 소개 드렸던 코딩 공부 웹 사이트 중 프로그래머스에서 제공되는 문제들을 풀이해주는 책이라 다시 추천으로 가져왔습니다. 또한 이번에 공부하면서 Baekjoon(백준)으로 도움을 받아 추천합니다!
안녕하세요! 멀티캠퍼스 유레카 3기 백엔드 과정을 수강 중인 개발자 지망생입니다.
**자료구조(Data Structure)**를 공부했어요! 그동안 코딩할 때 무의식적으로 배열을 쓰고, 리스트를 썼는데, 수업을 듣고 나니 왜 그 자료구조를 써야 하는지, 어떤 상황에 어떤 자료구조가 적합한지 완벽하게 이해하게 됐습니다.
"자료구조는 코딩의 기본기다. 배열, 스택, 큐, 트리... 이걸 모르면 효율적인 코드를 절대 짤 수 없어. 알고리즘 문제도 못 풀고, 실무에서도 고생한다!"
처음엔 "배열만 쓰면 되는 거 아닌가?"라고 생각했는데... 완전히 틀렸더라고요! 😅
특히 이진 탐색 트리(BST)를 배우면서 데이터 검색 속도가 얼마나 중요한지, 그리고 어떤 자료구조를 선택하느냐에 따라 프로그램 성능이 천지 차이라는 걸 체감했습니다!
🎯 Today I Learned
✅ 자료구조란 무엇인가?
✅ 배열(Array)의 특징과 한계
✅ 연결 리스트(Linked List)
✅ 스택(Stack) - LIFO 구조
✅ 큐(Queue) - FIFO 구조
✅ 트리(Tree) 기본 개념
✅ 이진 트리(Binary Tree)
✅ 이진 탐색 트리(Binary Search Tree)
✅ 각 자료구조의 시간 복잡도
🤔 자료구조, 왜 필요할까?
자료구조가 없다면?
// 학생 1000명의 성적을 관리한다고 가정
// ❌ 변수를 1000개 만들기?
int student1 = 85;
int student2 = 90;
int student3 = 78;
// ...
int student1000 = 92;
// 평균을 구하려면?
int sum = student1 + student2 + student3 + ... + student1000; // 😱
// 최고 점수를 찾으려면?
// 1000개를 일일이 비교? 불가능!
이렇게 하면 코드도 길어지고, 관리도 불가능하고, 효율도 최악이에요!
자료구조를 사용하면:
// ✅ 배열 사용
int[] students = new int[1000];
// 평균 구하기
int sum = 0;
for(int i = 0; i < students.length; i++) {
sum += students[i];
}
double average = sum / students.length;
// 최고 점수 찾기
int max = students[0];
for(int score : students) {
if(score > max) max = score;
}
훨씬 간결하고 효율적이죠!
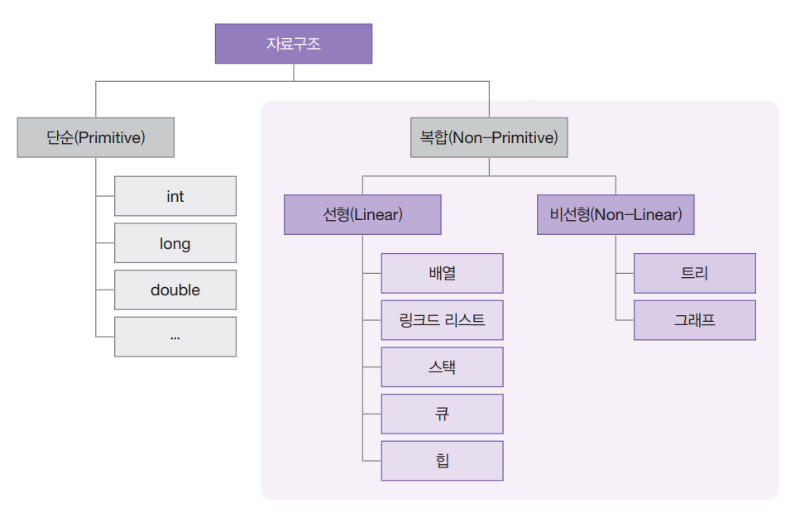
자료구조란?
자료구조 = 데이터를 효율적으로 저장하고 관리하는 방법
목적:
1. 메모리를 효율적으로 사용
2. 데이터 접근 속도 향상
3. 코드의 간결성과 가독성 향상
📦 1단계: 배열(Array) - 가장 기본적인 자료구조
배열이란?
배열 = 같은 타입의 데이터를 연속된 메모리 공간에 저장하는 자료구조
// 배열 선언
int[] numbers = new int[5]; // 크기 5인 배열
numbers[0] = 10;
numbers[1] = 20;
numbers[2] = 30;
numbers[3] = 40;
numbers[4] = 50;
// 또는
int[] numbers = {10, 20, 30, 40, 50};
메모리 구조:
Index: [0] [1] [2] [3] [4]
Value: 10 20 30 40 50
주소: 100 104 108 112 116 (4바이트씩)


배열의 특징
장점 단점
| ✅ 인덱스로 빠른 접근 (O(1)) | ❌ 크기 고정 (한번 정하면 변경 불가) |
| ✅ 메모리 연속 할당 (캐시 효율 좋음) | ❌ 삽입/삭제 느림 (O(n)) |
| ✅ 구현이 간단 | ❌ 메모리 낭비 가능 |
배열의 삽입/삭제가 느린 이유
// 배열 중간에 데이터 삽입
int[] arr = {10, 20, 30, 40, 50};
// index 2에 25를 삽입하려면?
// 1. 뒤의 모든 원소를 한 칸씩 이동 😰
arr[4] = arr[3]; // 50 이동
arr[3] = arr[2]; // 40 이동
arr[2] = 25; // 25 삽입
// 삭제도 마찬가지!
// index 2를 삭제하려면 뒤의 모든 원소를 앞으로 이동
결론: 배열은 읽기는 빠르지만, 쓰기(삽입/삭제)는 느리다!
배열 실전 예제
# Python으로 배열 다루기
# 배열 생성
students = [85, 90, 78, 92, 88]
# 접근 - O(1)
print(students[2]) # 78
# 추가 (끝에 추가) - O(1)
students.append(95)
# 삽입 (중간 삽입) - O(n)
students.insert(2, 100) # index 2에 100 삽입
# 삭제 - O(n)
students.pop(3) # index 3 삭제
# 검색 - O(n)
if 90 in students:
print("90점이 있습니다")
# 정렬 - O(n log n)
students.sort()
🔗 2단계: 연결 리스트(Linked List)
배열의 한계를 극복하다
문제: 배열은 크기가 고정되어 있어서 유연하지 못함
해결: 연결 리스트는 동적으로 크기 조절 가능!
연결 리스트란?
연결 리스트 = 각 노드가 데이터와 다음 노드의 주소를 가지는 자료구조
노드(Node) 구조:
┌────────┬────────┐
│ Data │ Next │ ← 하나의 노드
└────────┴────────┘
연결 리스트 구조:
Head → [10|●] → [20|●] → [30|●] → [40|null]


연결 리스트 구현
// 노드 클래스
class Node {
int data; // 데이터
Node next; // 다음 노드 참조
Node(int data) {
this.data = data;
this.next = null;
}
}
// 연결 리스트 클래스
class LinkedList {
Node head; // 첫 번째 노드
// 끝에 추가 - O(n)
void add(int data) {
Node newNode = new Node(data);
if(head == null) {
head = newNode;
return;
}
Node current = head;
while(current.next != null) {
current = current.next;
}
current.next = newNode;
}
// 중간에 삽입 - O(1) (위치를 안다면)
void insertAfter(Node prevNode, int data) {
if(prevNode == null) return;
Node newNode = new Node(data);
newNode.next = prevNode.next;
prevNode.next = newNode;
}
// 삭제 - O(n)
void delete(int data) {
if(head == null) return;
if(head.data == data) {
head = head.next;
return;
}
Node current = head;
while(current.next != null) {
if(current.next.data == data) {
current.next = current.next.next;
return;
}
current = current.next;
}
}
// 출력
void print() {
Node current = head;
while(current != null) {
System.out.print(current.data + " → ");
current = current.next;
}
System.out.println("null");
}
}
// 사용 예시
public class Main {
public static void main(String[] args) {
LinkedList list = new LinkedList();
list.add(10);
list.add(20);
list.add(30);
list.print(); // 10 → 20 → 30 → null
}
}
배열 vs 연결 리스트
구분 배열 연결 리스트
| 접근 | O(1) - 빠름 | O(n) - 느림 |
| 삽입/삭제 | O(n) - 느림 | O(1) - 빠름 (위치를 안다면) |
| 메모리 | 연속적 | 비연속적 |
| 크기 | 고정 | 동적 |
| 메모리 낭비 | 가능 | 포인터 공간 필요 |
📚 3단계: 스택(Stack) - 쌓아 올리기
스택이란?
스택 = 후입선출(LIFO: Last In First Out) 구조
마지막에 들어간 데이터가 가장 먼저 나옴
실생활 비유:
- 접시 쌓기: 맨 위에 놓은 접시를 먼저 꺼냄
- 브라우저 뒤로 가기: 가장 최근에 본 페이지로 돌아감
- Ctrl+Z (실행 취소): 가장 최근 작업을 취소

스택의 주요 연산
push(): 데이터를 스택의 맨 위에 추가
pop(): 스택의 맨 위 데이터를 제거하고 반환
peek(): 스택의 맨 위 데이터를 확인 (제거 X)
isEmpty(): 스택이 비어있는지 확인
스택 구현 (배열 사용)
# Python으로 스택 구현
class Stack:
def __init__(self):
self.items = []
def push(self, item):
self.items.append(item)
print(f"Push: {item}")
def pop(self):
if not self.is_empty():
item = self.items.pop()
print(f"Pop: {item}")
return item
print("Stack is empty!")
def peek(self):
if not self.is_empty():
return self.items[-1]
return None
def is_empty(self):
return len(self.items) == 0
def size(self):
return len(self.items)
def print_stack(self):
print("Stack:", self.items)
# 사용 예시
stack = Stack()
stack.push(10) # [10]
stack.push(20) # [10, 20]
stack.push(30) # [10, 20, 30]
stack.print_stack() # Stack: [10, 20, 30]
print("Top:", stack.peek()) # Top: 30
stack.pop() # 30 제거 → [10, 20]
stack.pop() # 20 제거 → [10]
stack.print_stack() # Stack: [10]
스택 활용 예시
1. 괄호 짝 맞추기
def is_balanced(expression):
stack = []
pairs = {')': '(', '}': '{', ']': '['}
for char in expression:
if char in '({[':
stack.append(char)
elif char in ')}]':
if not stack or stack[-1] != pairs[char]:
return False
stack.pop()
return len(stack) == 0
print(is_balanced("((()))")) # True
print(is_balanced("((()")) # False
print(is_balanced("({[]})")) # True
2. 브라우저 뒤로 가기
class BrowserHistory {
constructor() {
this.backStack = []; // 뒤로 가기 스택
this.currentPage = null;
}
visit(url) {
if(this.currentPage) {
this.backStack.push(this.currentPage);
}
this.currentPage = url;
console.log(`방문: ${url}`);
}
back() {
if(this.backStack.length > 0) {
this.currentPage = this.backStack.pop();
console.log(`뒤로 가기: ${this.currentPage}`);
} else {
console.log("더 이상 뒤로 갈 수 없습니다");
}
}
}
// 사용
const browser = new BrowserHistory();
browser.visit("google.com"); // 방문: google.com
browser.visit("youtube.com"); // 방문: youtube.com
browser.visit("github.com"); // 방문: github.com
browser.back(); // 뒤로 가기: youtube.com
browser.back(); // 뒤로 가기: google.com
🚶 4단계: 큐(Queue) - 줄 서기
큐란?
큐 = 선입선출(FIFO: First In First Out) 구조
먼저 들어간 데이터가 먼저 나옴
실생활 비유:
- 은행 대기 줄: 먼저 온 사람이 먼저 서비스 받음
- 프린터 출력 대기열
- 게임 매칭 시스템

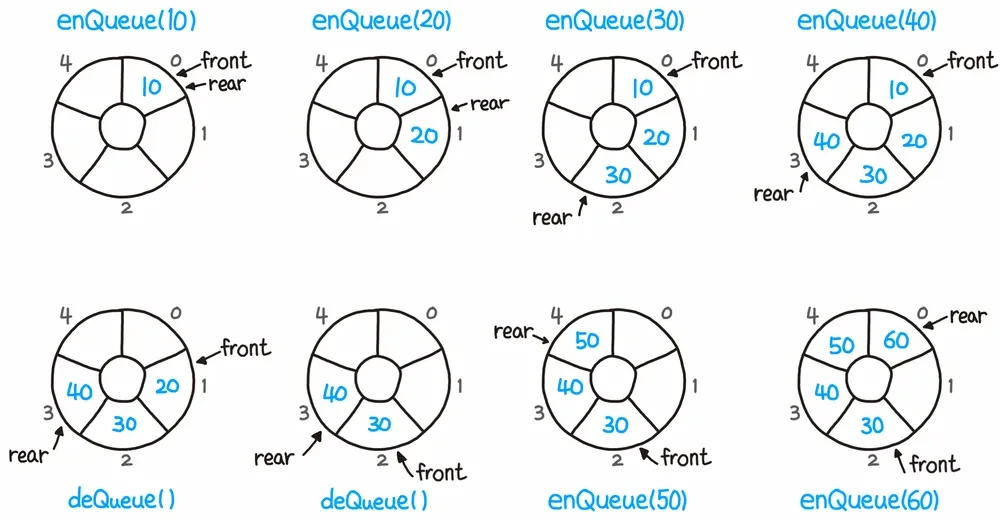
큐의 주요 연산
enqueue(): 큐의 뒤(rear)에 데이터 추가
dequeue(): 큐의 앞(front)에서 데이터 제거 및 반환
front(): 큐의 맨 앞 데이터 확인
isEmpty(): 큐가 비어있는지 확인
큐 구현
import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
public static void main(String[] args) {
Queue<String> queue = new LinkedList<>();
// Enqueue
queue.offer("손님1");
queue.offer("손님2");
queue.offer("손님3");
System.out.println("Queue: " + queue); // [손님1, 손님2, 손님3]
// Front 확인
System.out.println("Front: " + queue.peek()); // 손님1
// Dequeue
System.out.println("서비스: " + queue.poll()); // 손님1
System.out.println("서비스: " + queue.poll()); // 손님2
System.out.println("Queue: " + queue); // [손님3]
}
}
원형 큐(Circular Queue)
일반 큐의 문제점:
문제: 배열로 큐를 구현하면 앞쪽 공간이 낭비됨
[X][X][X][데이터1][데이터2]
↑
front가 계속 뒤로 이동하면 앞 공간 낭비!
해결: 원형 큐 - 배열의 끝과 시작을 연결!
class CircularQueue:
def __init__(self, size):
self.size = size
self.queue = [None] * size
self.front = 0
self.rear = 0
def enqueue(self, item):
next_rear = (self.rear + 1) % self.size
if next_rear == self.front:
print("Queue is full!")
return
self.queue[self.rear] = item
self.rear = next_rear
def dequeue(self):
if self.is_empty():
print("Queue is empty!")
return None
item = self.queue[self.front]
self.queue[self.front] = None
self.front = (self.front + 1) % self.size
return item
def is_empty(self):
return self.front == self.rear
스택 vs 큐 비교

구분 스택(Stack) 큐(Queue)
| 구조 | LIFO (후입선출) | FIFO (선입선출) |
| 삽입 | push (top에) | enqueue (rear에) |
| 삭제 | pop (top에서) | dequeue (front에서) |
| 활용 | 실행 취소, 뒤로 가기, DFS | 대기열, 프린터, BFS |
🌳 5단계: 트리(Tree) - 계층 구조
트리란?
트리 = 노드들이 계층적으로 연결된 자료구조
부모-자식 관계를 가짐
실생활 비유:
- 조직도
- 파일 시스템
- HTML DOM 구조

트리 용어
A ← Root (루트): 최상위 노드
/ \
B C ← B, C: A의 자식(Child)
/ \ \ A: B, C의 부모(Parent)
D E F ← Leaf (리프): 자식이 없는 노드
레벨 0: A
레벨 1: B, C
레벨 2: D, E, F
높이(Height): 3 (루트부터 가장 깊은 리프까지)
주요 용어:
- Root: 최상위 노드
- Parent: 부모 노드
- Child: 자식 노드
- Leaf: 자식이 없는 노드
- Sibling: 같은 부모를 가진 노드
- Level: 루트로부터의 거리
- Height: 트리의 최대 레벨
- Degree: 자식 노드의 개수
🌲 6단계: 이진 트리(Binary Tree)
이진 트리란?
이진 트리 = 각 노드가 최대 2개의 자식을 가지는 트리
이진 트리의 종류
1. 포화 이진 트리(Full Binary Tree)
A
/ \
B C
/ \ / \
D E F G
모든 레벨이 꽉 찬 트리
노드 개수 = 2^h - 1 (h: 높이)
2. 완전 이진 트리(Complete Binary Tree)
A
/ \
B C
/ \ /
D E F
마지막 레벨을 제외하고 모든 레벨이 꽉 참
마지막 레벨은 왼쪽부터 차 있음
3. 편향 이진 트리(Skewed Binary Tree)
A
\
B
\
C
한쪽으로만 자식이 있는 트리
(연결 리스트와 비슷)
이진 트리 순회(Traversal)
1. 전위 순회(Pre-order): 루트 → 왼쪽 → 오른쪽
def preorder(node):
if node:
print(node.data, end=' ') # 루트
preorder(node.left) # 왼쪽
preorder(node.right) # 오른쪽
2. 중위 순회(In-order): 왼쪽 → 루트 → 오른쪽
def inorder(node):
if node:
inorder(node.left) # 왼쪽
print(node.data, end=' ') # 루트
inorder(node.right) # 오른쪽
3. 후위 순회(Post-order): 왼쪽 → 오른쪽 → 루트
def postorder(node):
if node:
postorder(node.left) # 왼쪽
postorder(node.right) # 오른쪽
print(node.data, end=' ') # 루트
예시:
4
/ \
2 6
/ \ / \
1 3 5 7
전위 순회: 4 2 1 3 6 5 7
중위 순회: 1 2 3 4 5 6 7 (정렬된 순서!)
후위 순회: 1 3 2 5 7 6 4
🔍 7단계: 이진 탐색 트리(Binary Search Tree, BST)
이진 탐색 트리란?
이진 탐색 트리 = 이진 트리 + 정렬 규칙
규칙:
1. 왼쪽 자식 < 부모 노드
2. 오른쪽 자식 > 부모 노드
3. 모든 서브트리도 이진 탐색 트리
예시:
20
/ \
15 25
/ \ \
10 18 30
/
5
✅ 왼쪽은 모두 20보다 작음 (10, 15, 18, 5)
✅ 오른쪽은 모두 20보다 큼 (25, 30)

왜 이진 탐색 트리를 사용할까?
배열의 문제:
정렬된 배열: [5, 10, 15, 20, 25, 30]
검색: O(log n) - 이진 탐색 가능 ✅
삽입: O(n) - 뒤의 원소를 모두 이동 ❌
삭제: O(n) - 뒤의 원소를 모두 이동 ❌
연결 리스트의 문제:
연결 리스트: 5 → 10 → 15 → 20 → 25 → 30
검색: O(n) - 순차 검색 ❌
삽입: O(1) - 위치만 안다면 ✅
삭제: O(1) - 위치만 안다면 ✅
이진 탐색 트리:
검색: O(log n) ✅
삽입: O(log n) ✅
삭제: O(log n) ✅
배열과 연결 리스트의 장점만 합침!
BST 검색(Search)
class Node {
int data;
Node left, right;
Node(int data) {
this.data = data;
left = right = null;
}
}
class BST {
Node root;
// 검색 - O(log n)
Node search(Node node, int key) {
// 1. 노드가 null이거나 key를 찾았으면 반환
if (node == null || node.data == key) {
return node;
}
// 2. key가 작으면 왼쪽 서브트리 탐색
if (key < node.data) {
return search(node.left, key);
}
// 3. key가 크면 오른쪽 서브트리 탐색
return search(node.right, key);
}
}
검색 과정 예시:
26을 찾기:
20 20과 비교: 26 > 20 → 오른쪽
/ \
15 25 25와 비교: 26 > 25 → 오른쪽
/ \ \
10 18 30 30과 비교: 26 < 30 → 왼쪽
/ /
5 26 26 찾음! ✅
BST 삽입(Insert)
// 삽입 - O(log n)
Node insert(Node node, int data) {
// 1. 빈 자리를 찾으면 새 노드 생성
if (node == null) {
return new Node(data);
}
// 2. 작으면 왼쪽, 크면 오른쪽으로 이동
if (data < node.data) {
node.left = insert(node.left, data);
} else if (data > node.data) {
node.right = insert(node.right, data);
}
return node;
}
삽입 과정 예시:
16을 삽입:
20 20과 비교: 16 < 20 → 왼쪽
/ \
15 25 15와 비교: 16 > 15 → 오른쪽
/ \ \
10 18 30 18과 비교: 16 < 18 → 왼쪽
/
5
빈 자리 발견! 16 삽입 ✅
결과:
20
/ \
15 25
/ \ \
10 18 30
/ /
5 16 ← 새로 삽입!
BST 삭제(Delete)
삭제는 3가지 경우가 있어요!
Case 1: 리프 노드 삭제
20
/ \
15 25
/ \
10 18
10 삭제 → 그냥 제거하면 됨!
20
/ \
15 25
\
18
Case 2: 자식이 하나인 노드 삭제
20
/ \
15 25
\ \
18 30
25 삭제 → 자식(30)을 부모(20)에 연결
20
/ \
15 30
\
18
Case 3: 자식이 둘인 노드 삭제 (가장 복잡!)
20
/ \
15 25
/ \ \
10 18 30
15 삭제:
1. 오른쪽 서브트리의 최솟값(18) 찾기
2. 15를 18로 교체
3. 원래 18 위치 삭제
20
/ \
18 25
/ \
10 30
// 삭제 구현
Node delete(Node node, int key) {
if (node == null) return null;
// 삭제할 노드 찾기
if (key < node.data) {
node.left = delete(node.left, key);
} else if (key > node.data) {
node.right = delete(node.right, key);
} else {
// Case 1: 리프 노드
if (node.left == null && node.right == null) {
return null;
}
// Case 2: 자식이 하나
else if (node.left == null) {
return node.right;
} else if (node.right == null) {
return node.left;
}
// Case 3: 자식이 둘
else {
Node successor = findMin(node.right);
node.data = successor.data;
node.right = delete(node.right, successor.data);
}
}
return node;
}
// 최솟값 찾기 (가장 왼쪽 노드)
Node findMin(Node node) {
while (node.left != null) {
node = node.left;
}
return node;
}
BST의 시간 복잡도
균형 잡힌 트리:
20
/ \
15 25
/ \ / \
10 18 23 30
높이 = log n
검색, 삽입, 삭제 = O(log n) ✅
편향된 트리 (최악의 경우):
5
\
10
\
15
\
20
높이 = n
검색, 삽입, 삭제 = O(n) ❌
연결 리스트와 동일...
해결책: AVL 트리, 레드-블랙 트리 같은 균형 이진 탐색 트리 사용!
📊 자료구조 선택 가이드
상황별 최적의 자료구조
상황 추천 자료구조 이유
| 빠른 접근만 필요 | 배열(Array) | O(1) 접근 |
| 빈번한 삽입/삭제 | 연결 리스트(Linked List) | O(1) 삽입/삭제 |
| 실행 취소 기능 | 스택(Stack) | LIFO 구조 |
| 대기열 처리 | 큐(Queue) | FIFO 구조 |
| 계층 구조 표현 | 트리(Tree) | 부모-자식 관계 |
| 빠른 검색 + 정렬 | 이진 탐색 트리(BST) | O(log n) 검색 |
시간 복잡도 비교표
자료구조 접근 검색 삽입 삭제
| 배열 | O(1) | O(n) | O(n) | O(n) |
| 연결 리스트 | O(n) | O(n) | O(1)* | O(1)* |
| 스택 | O(n) | O(n) | O(1) | O(1) |
| 큐 | O(n) | O(n) | O(1) | O(1) |
| BST | O(log n) | O(log n) | O(log n) | O(log n) |
*위치를 아는 경우
💡 오늘 나는 무엇을 잘했는가 (성취)
모든 자료구조를 직접 구현해봄!
수업 시간에 배운 7가지 자료구조를 모두 코드로 구현해봤어요. 특히 이진 탐색 트리의 삽입, 삭제 로직을 처음엔 이해하기 어려웠는데, 디버깅하면서 하나하나 따라가니까 완전히 이해가 됐습니다!
// 내가 직접 짠 BST 삽입 코드!
Node insert(Node node, int data) {
if (node == null) {
return new Node(data);
}
if (data < node.data) {
node.left = insert(node.left, data);
} else {
node.right = insert(node.right, data);
}
return node;
}
처음 짰을 때는 재귀가 이해 안 됐는데, 종이에 트리를 그리면서 따라가니까 "아!"하고 깨달았어요.
알고리즘 문제 풀이 성공
백준 문제 중 스택을 활용하는 "괄호 짝 맞추기" 문제를 혼자 힘으로 풀었어요! 수업 전에는 어떻게 풀어야 할지 감도 안 잡혔는데, 스택 개념을 배우고 나니 "아, 이건 스택으로 풀면 되겠네!"하고 바로 접근법이 떠올랐습니다.
🔧 어떤 문제를 겪었고, 어떻게 개선할까 (개선점)
문제 1: BST 삭제 로직이 너무 복잡함
3가지 경우를 다 고려해야 해서 코드가 복잡하고 헷갈렸어요. 특히 자식이 2개인 노드를 삭제할 때 "왜 오른쪽 서브트리의 최솟값을 찾아야 하지?"가 이해 안 됐어요.
개선 계획:
1. 종이에 트리를 그리면서 단계별로 시뮬레이션
2. 각 Case마다 예제를 3개씩 더 풀어보기
3. "후계자(Successor)" 개념 완벽히 이해하기
그림으로 그려보니까 이해가 훨씬 쉬웠어요!
문제 2: 재귀 호출이 아직 어색함
트리 순회할 때 재귀 함수가 어떻게 작동하는지 헷갈렸어요. 특히 "재귀 호출이 끝나고 어디로 돌아가는가?"가 계속 헷갈렸습니다.
해결 방법:
# 디버깅 출력을 넣어서 호출 순서 확인!
def inorder(node, depth=0):
if node:
print(" " * depth + f"왼쪽 탐색: {node.data}")
inorder(node.left, depth + 1)
print(" " * depth + f"출력: {node.data}")
print(" " * depth + f"오른쪽 탐색: {node.data}")
inorder(node.right, depth + 1)
실행 흐름을 직접 보니까 재귀가 어떻게 작동하는지 명확해졌어요!
문제 3: 언제 어떤 자료구조를 써야 하는지 판단이 어려움
"이 문제는 스택으로 풀어야 하나? 큐로 풀어야 하나?"가 헷갈렸어요.
판단 기준 정리:
LIFO (나중 것 먼저) → 스택
- 실행 취소
- 뒤로 가기
- DFS (깊이 우선 탐색)
FIFO (먼저 온 것 먼저) → 큐
- 대기 줄
- BFS (너비 우선 탐색)
- 작업 스케줄링
정렬된 데이터 + 빠른 검색 → BST
- 전화번호부
- 사전
📚 오늘 배운 것 (학습)
1. 자료구조 = 문제 해결의 도구
문제: "최근 방문한 10개 페이지를 저장하고 싶다"
생각 과정:
1. 새 페이지 방문 → 맨 뒤에 추가
2. 10개 초과 → 가장 오래된 것 삭제
3. FIFO 구조네?
→ 큐 사용!
문제: "작업을 취소하고 싶다"
생각 과정:
1. 가장 최근 작업을 취소
2. LIFO 구조네?
→ 스택 사용!
자료구조를 알면 어떤 도구를 써야 하는지 판단할 수 있어요!
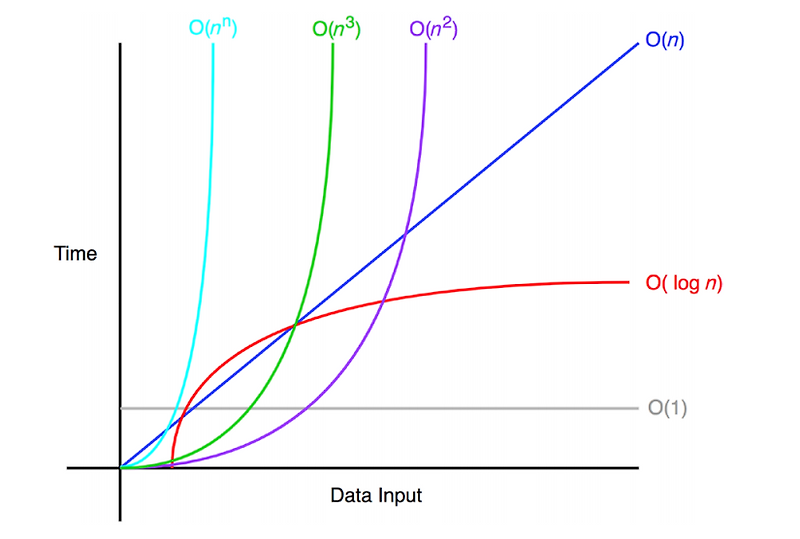
2. 시간 복잡도의 중요성
데이터 1만 개일 때:
O(n) = 10,000번 연산
O(log n) = 14번 연산
O(n²) = 100,000,000번 연산
데이터가 많아질수록 차이가 엄청남!
그래서 상황에 맞는 자료구조 선택이 중요한 거예요!
3. Trade-off (상충 관계)
배열:
- 접근 빠름 (O(1)) ✅
- 삽입/삭제 느림 (O(n)) ❌
연결 리스트:
- 삽입/삭제 빠름 (O(1)) ✅
- 접근 느림 (O(n)) ❌
완벽한 자료구조는 없다!
상황에 맞게 선택해야 한다!
4. 공간 복잡도도 중요하다
배열: 크기만큼만 메모리 사용
연결 리스트:
- 데이터 + 포인터(주소) 저장
- 메모리를 더 많이 사용
트레이드오프:
- 시간을 줄이려면 공간을 더 쓰고
- 공간을 줄이려면 시간이 더 걸림
😊 좋았던 점 & 😅 아쉬웠던 점
좋았던 점
👍 그림으로 설명해주셔서 이해가 쉬웠음
특히 트리 구조를 칠판에 그리면서 설명해주셨는데, 말로만 들었으면 절대 이해 못 했을 것 같아요. 스택과 큐도 "접시 쌓기", "은행 줄 서기" 같은 실생활 비유로 설명해주셔서 기억에 잘 남았습니다!
👍 코드 예제가 풍부함
Java, Python, JavaScript로 다양하게 구현 예제를 보여주셔서 좋았어요. 제가 Python을 주로 쓰는데, Java 예제도 읽으면서 언어별 차이를 배울 수 있었습니다.
👍 "왜 필요한가?"를 먼저 설명
단순히 "이게 스택이다"가 아니라 "배열의 문제점 → 연결 리스트 등장"처럼 흐름이 있어서 이해가 훨씬 빨랐어요. 특히 BST가 왜 배열과 연결 리스트의 장점을 합친 건지 명확히 이해됐습니다!
아쉬웠던 점
😢 실습 시간 부족
이론은 충분히 배웠는데, 실제로 코드를 짜보는 시간이 부족했어요. 특히 BST는 구현이 복잡해서 한 번에 이해가 안 됐어요. 수업 시간에 30분 정도 코딩 실습 시간이 있었으면 좋았을 것 같아요.
😢 고급 자료구조는 다루지 못함
AVL 트리, 레드-블랙 트리, 힙(Heap) 같은 고급 자료구조는 시간 관계상 다루지 못했어요. 특히 "편향 트리 문제를 어떻게 해결하는가?"가 궁금한데 답을 못 들었습니다.
😢 실무 사례가 더 있었으면
"이 자료구조가 실제 서비스에서 어떻게 쓰이는가?"에 대한 예시가 더 있으면 좋았을 것 같아요. 예를 들어 "YouTube의 재생 목록은 어떤 자료구조로 구현됐을까?" 같은 것들요!
🎓 나만의 학습 팁
1. 그림 그리기!
트리를 이해하려면 무조건 종이에 그려보세요!
20
/ \
15 25
/ \ \
10 18 30
30을 삭제하면?
18을 삽입하면?
26을 검색하면?
직접 그리면서 시뮬레이션하면 100% 이해됨!
저는 A4 용지에 트리를 20번 넘게 그렸어요.
2. 시간 복잡도 체감하기
import time
# 배열에서 검색 - O(n)
arr = list(range(1000000))
start = time.time()
999999 in arr
print(f"배열 검색: {time.time() - start}초")
# BST에서 검색 - O(log n)
# (실제로 BST 구현해서 테스트)
직접 시간을 재보면 "O(log n)이 왜 빠른가?"를 체감할 수 있어요!
3. 문제 풀이로 실력 향상

초급:
- 백준 10828: 스택 구현
- 백준 10845: 큐 구현
- 백준 9012: 괄호 짝 맞추기
중급:
- 백준 1158: 요세푸스 문제 (큐)
- 백준 1918: 후위 표기식 (스택)
- 백준 5639: 이진 검색 트리 (BST)
문제를 풀면서 "이 문제는 어떤 자료구조를 써야 하나?"를 고민하는 게 진짜 공부예요!
4. 라이브러리 코드 읽어보기
# Python의 리스트는 어떻게 구현됐을까?
# GitHub에서 CPython 소스 코드 확인!
import collections
# deque는 어떻게 구현됐을까?
# 양방향 연결 리스트로 구현!
실제 라이브러리 코드를 보면 "프로들은 이렇게 구현하는구나!"를 배울 수 있어요.
5. 비교 정리하기
## 스택 vs 큐
| 구분 | 스택 | 큐 |
|------|------|-----|
| 구조 | LIFO | FIFO |
| 사용 | 실행 취소 | 대기열 |
## 배열 vs 연결 리스트
| 구분 | 배열 | 연결 리스트 |
|------|------|------------|
| 접근 | O(1) | O(n) |
| 삽입 | O(n) | O(1) |
이렇게 비교표를 만들어두면 헷갈릴 때 바로 찾아볼 수 있어요!
🚀 다음 학습 목표
📌 단기 목표 (이번 주)
✓ BST 삽입/삭제 알고리즘 완벽히 이해
✓ 백준 자료구조 문제 10개 풀기
✓ 각 자료구조를 Python으로 직접 구현
✓ 시간 복잡도 측정 프로그램 만들기
📌 중기 목표 (이번 달)
✓ 힙(Heap) 자료구조 공부
✓ AVL 트리, 레드-블랙 트리 공부
✓ 해시 테이블 공부
✓ 그래프 자료구조 공부
✓ DFS, BFS 알고리즘 구현
📌 장기 목표 (부트캠프 기간)
✓ 코딩 테스트 대비 자료구조 완벽 정리
✓ 포트폴리오에 자료구조 시각화 프로그램 추가
✓ 알고리즘 문제 100개 이상 풀기
🎬 마치며
수업을 듣기 전에는 "자료구조? 배열만 쓰면 되는 거 아니야?"라고 생각했어요.
하지만 하나하나 배우면서 깨달은 게 있습니다.
자료구조는 단순히 '데이터를 저장하는 방법'이 아니라, '문제를 효율적으로 해결하는 도구'입니다.
같은 기능을 구현해도:
배열: 1초 걸림
BST: 0.001초 걸림
1000배 차이!
특히 이진 탐색 트리를 배우면서 **"정렬과 검색을 동시에 효율적으로 할 수 있다"**는 게 정말 신기했어요. 왼쪽은 작고 오른쪽은 크다는 단순한 규칙만으로도 엄청난 성능 향상을 이룰 수 있다니!
그리고 스택과 큐가 실생활의 많은 문제들을 모델링한다는 것도 인상 깊었어요. "브라우저 뒤로 가기"가 스택이고, "프린터 대기열"이 큐라는 걸 알고 나니, 앞으로는 일상에서도 "이건 어떤 자료구조로 구현됐을까?"를 생각하게 될 것 같아요.
앞으로는 단순히 "작동하는 코드"가 아니라 **"효율적인 코드"**를 짜는 개발자가 되고 싶어요! 💪
💬 여러분이 가장 좋아하는 자료구조는?
어떤 자료구조가 가장 유용했나요? 실무나 알고리즘 문제에서 자주 쓰는 자료구조 공유해주세요! 🙏